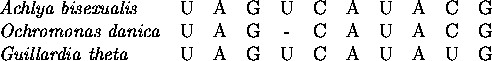


Next: Parallele Computerplattformen und Parallelrechnen
Up: Phylogenie
Previous: Evolutionsmodelle
Zur Rekonstruktion phylogenetischer Bäume aus Sequenzdaten
biologischer Makromoleküle haben sich verschiedene
Methoden etabliert.
Diese lassen sich allgemein in zwei Gruppen unterteilen, in
distanzbasierte und merkmalsbasierte Methoden.
(Felsenstein, 1982; Swofford and Olsen, 1990; Waterman, 1995; Weir, 1990)
Bei den distanzbasierten Methoden
wird für alle Sequenzpaare eine evolutionäre Distanz
berechnet. Im einfachsten Fall ist dies
die Hammingdistanz (Cormen et al., 1990), bei der die Anzahl der
sich unterscheidenden Basen zweier Sequenzen aufsummiert wird.
Die errechnete Distanzmatrix dient als Grundlage zur
Konstruktion des Stammbaumes.
Hierfür werden zumeist Clustering-Verfahren verwendet
(Kap. 1.4.1).
An dieser Methode wird kritisiert, daß die vorhandenen
Sequenzdaten zur Berechnung des Baumes auf die Distanzen
reduziert werden.
(Fitch and Margoliash, 1967; Saitou and Nei, 1987)
Wichtige Vertreter der merkmalsbasierten Methoden sind
die Maximum-Parsimony-Methode![[*]](foot_motif.gif) und der Maximum-Likelihood-Ansatz.
Das Maximum-Parsimony-Verfahren
konstruiert für alle internen Knoten eines vorgegebenen Stammbaumes
Sequenzen, die die von diesen Knoten repräsentierten Organismen
gehabt haben könnten. Diese Sequenzen werden so konstruiert,
daß die Sequenzen entlang des Baumes, während der vom Stammbaum
vorgegebenen evolutionären Entwicklung, möglichst wenigen
Mutationen unterworfen sind. Die Gesamtsumme aller im Baum nötigen
Mutationen ist dann das Maß für die Qualität des Baumes.
Von der Maximum-Parsimony-Methode wird versucht,
aus allen möglichen Stammbäumen denjenigen zu finden, für den
die geringste Anzahl an Mutationen nötig ist.
Diese Methode wurde ursprünglich für morphologische Daten entworfen
und hat sich bewährt, wenn sich die beobachteten Merkmale nur selten
ändern. Das gilt im allgemeinen für morphologische Daten.
Diese Methode scheitert jedoch, wenn die beobachteten Merkmale hochvariabel
sind oder sehr lange Kanten im gesuchten Baum vorkommen.
(Swofford and Olsen, 1990; Waterman, 1995)
und der Maximum-Likelihood-Ansatz.
Das Maximum-Parsimony-Verfahren
konstruiert für alle internen Knoten eines vorgegebenen Stammbaumes
Sequenzen, die die von diesen Knoten repräsentierten Organismen
gehabt haben könnten. Diese Sequenzen werden so konstruiert,
daß die Sequenzen entlang des Baumes, während der vom Stammbaum
vorgegebenen evolutionären Entwicklung, möglichst wenigen
Mutationen unterworfen sind. Die Gesamtsumme aller im Baum nötigen
Mutationen ist dann das Maß für die Qualität des Baumes.
Von der Maximum-Parsimony-Methode wird versucht,
aus allen möglichen Stammbäumen denjenigen zu finden, für den
die geringste Anzahl an Mutationen nötig ist.
Diese Methode wurde ursprünglich für morphologische Daten entworfen
und hat sich bewährt, wenn sich die beobachteten Merkmale nur selten
ändern. Das gilt im allgemeinen für morphologische Daten.
Diese Methode scheitert jedoch, wenn die beobachteten Merkmale hochvariabel
sind oder sehr lange Kanten im gesuchten Baum vorkommen.
(Swofford and Olsen, 1990; Waterman, 1995)
Der anerkannteste Ansatz basiert auf der von Fisher (1912) eingeführten
Maximum-Likelihood-Methode![[*]](foot_motif.gif) (Kreyszig, 1975).
Die Maximum-Likelihood-Methode wird benutzt, um unbekannte
Parameter zu schätzen, von denen eine bekannte Wahrscheinlichkeitsfunktion
für einen stochastischen Prozeß abhängt.
Mit dieser Methode werden dann anhand einer festen
Stichprobe, in unserem Fall der Sequenzdaten, die unbekannten Parameter so
geschätzt, daß der Wert der Wahrscheinlichkeitsfunktion,
bei fester Stichprobe als Likelihood-Funktion bezeichnet,
sein Maximum erreicht.
Die in der Stammbaumanalyse zu schätzenden unbekannten Parameter
sind die Kantenlängen in einem vorgegebenen Baum.
(Goldman, 1990; Kreyszig, 1975)
(Kreyszig, 1975).
Die Maximum-Likelihood-Methode wird benutzt, um unbekannte
Parameter zu schätzen, von denen eine bekannte Wahrscheinlichkeitsfunktion
für einen stochastischen Prozeß abhängt.
Mit dieser Methode werden dann anhand einer festen
Stichprobe, in unserem Fall der Sequenzdaten, die unbekannten Parameter so
geschätzt, daß der Wert der Wahrscheinlichkeitsfunktion,
bei fester Stichprobe als Likelihood-Funktion bezeichnet,
sein Maximum erreicht.
Die in der Stammbaumanalyse zu schätzenden unbekannten Parameter
sind die Kantenlängen in einem vorgegebenen Baum.
(Goldman, 1990; Kreyszig, 1975)
Diese Methode wird in dieser Arbeit verwendet und ist in
Kap. 4.2 ausführlich beschrieben.
Der Vorteil dieser Methode liegt darin, daß
unter Berücksichtigung eines expliziten Evolutionsmodells bei der
Berechnung der Stammbäume die vollständigen Daten
in die Analyse mit eingehen.
Der Hauptnachteil der ML-Methode ist, daß enorme Rechenzeiten
nötig sind, um die große Anzahl der möglichen Stammbäume
zu überprüfen,
die auch bei heuristischen Methoden meist exponentiell mit der
Anzahl der benutzten Spezies wächst.
(Felsenstein, 1981; Swofford and Olsen, 1990)
Abbildung:
Ausschnitt aus dem Alignment von
18S rRNA-Sequenzen aus dem Zellkern
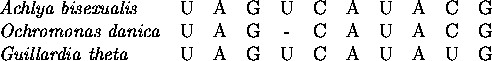 |
Die meisten merkmalsbasierten Methoden, die Sequenzen biologischer
Makromoleküle benutzen, benötigten von diesen Sequenzen ein
Alignment![[*]](foot_motif.gif) .
In einem solchen Alignment stehen die homologen Merkmale (hier
organische Basen oder Aminosäuren) in Spalten untereinander für
jede zu untersuchende Spezies. Alle Sequenzmerkmale einer Spezies stehen
hierbei in einer Zeile (Abb. 1.6).
In einem solchen Alignment lassen sich Mutationen ablesen, die zwischen zwei
Sequenzen liegen, z.B. ist wahrscheinlich zwischen
Ochromonas danica und den beiden anderen Spezies
bei Spalte 4 irgendwann einmal ein Indel und
zwischen Guillardia theta und den anderen eine Substitution
(
.
In einem solchen Alignment stehen die homologen Merkmale (hier
organische Basen oder Aminosäuren) in Spalten untereinander für
jede zu untersuchende Spezies. Alle Sequenzmerkmale einer Spezies stehen
hierbei in einer Zeile (Abb. 1.6).
In einem solchen Alignment lassen sich Mutationen ablesen, die zwischen zwei
Sequenzen liegen, z.B. ist wahrscheinlich zwischen
Ochromonas danica und den beiden anderen Spezies
bei Spalte 4 irgendwann einmal ein Indel und
zwischen Guillardia theta und den anderen eine Substitution
( , bzw.
, bzw.  auf DNA-Ebene)
in Spalte 9 aufgetreten.
Die hier abzulesenden Mutationen sind allerdings nur die offensichtlichen
Mutationen.
Wieviele Hin- und Rückmutationen es während der
Entwicklungsgeschichte gegeben hat und welche Sequenzen die
Vorfahren der untersuchten Spezies hatten, können wir heute nicht
mehr feststellen. Auch liegen die Sequenzen der Makromoleküle,
die wir untersuchen, nach dem Sequenzieren oder der Datenbankrecherche
nur als einzelne Buchstabenfolgen vor. Diese zu alignieren, ist
ein anderes hervorstechendes Problem, an dem zur Zeit in der Bioinformatik
gearbeitet wird. Die meisten Programme zum Alignieren von Sequenzen
bringen nur sehr unbefriedigende Ergebnisse, so daß nahezu alle
erhaltenen Alignments noch von Hand nachgebessert werden müssen
bzw. viele Alignments von vorneherein von Hand angefertigt werden.
auf DNA-Ebene)
in Spalte 9 aufgetreten.
Die hier abzulesenden Mutationen sind allerdings nur die offensichtlichen
Mutationen.
Wieviele Hin- und Rückmutationen es während der
Entwicklungsgeschichte gegeben hat und welche Sequenzen die
Vorfahren der untersuchten Spezies hatten, können wir heute nicht
mehr feststellen. Auch liegen die Sequenzen der Makromoleküle,
die wir untersuchen, nach dem Sequenzieren oder der Datenbankrecherche
nur als einzelne Buchstabenfolgen vor. Diese zu alignieren, ist
ein anderes hervorstechendes Problem, an dem zur Zeit in der Bioinformatik
gearbeitet wird. Die meisten Programme zum Alignieren von Sequenzen
bringen nur sehr unbefriedigende Ergebnisse, so daß nahezu alle
erhaltenen Alignments noch von Hand nachgebessert werden müssen
bzw. viele Alignments von vorneherein von Hand angefertigt werden.
Die Ergebnisse der Stammbaumanalysen hängen sehr von der Qualität der
benutzten Alignments ab. Daher ist es wichtig, Alignments zu benutzen,
die möglichst fehlerfrei sind. Über dieses Problem wird noch später
im Kapitel 1.8
über rRNA-Sequenzen gesprochen.



Next: Parallele Computerplattformen und Parallelrechnen
Up: Phylogenie
Previous: Evolutionsmodelle
Heiko Schmidt
7/17/1997
![[*]](foot_motif.gif) und der Maximum-Likelihood-Ansatz.
Das Maximum-Parsimony-Verfahren
konstruiert für alle internen Knoten eines vorgegebenen Stammbaumes
Sequenzen, die die von diesen Knoten repräsentierten Organismen
gehabt haben könnten. Diese Sequenzen werden so konstruiert,
daß die Sequenzen entlang des Baumes, während der vom Stammbaum
vorgegebenen evolutionären Entwicklung, möglichst wenigen
Mutationen unterworfen sind. Die Gesamtsumme aller im Baum nötigen
Mutationen ist dann das Maß für die Qualität des Baumes.
Von der Maximum-Parsimony-Methode wird versucht,
aus allen möglichen Stammbäumen denjenigen zu finden, für den
die geringste Anzahl an Mutationen nötig ist.
Diese Methode wurde ursprünglich für morphologische Daten entworfen
und hat sich bewährt, wenn sich die beobachteten Merkmale nur selten
ändern. Das gilt im allgemeinen für morphologische Daten.
Diese Methode scheitert jedoch, wenn die beobachteten Merkmale hochvariabel
sind oder sehr lange Kanten im gesuchten Baum vorkommen.
(Swofford and Olsen, 1990; Waterman, 1995)
und der Maximum-Likelihood-Ansatz.
Das Maximum-Parsimony-Verfahren
konstruiert für alle internen Knoten eines vorgegebenen Stammbaumes
Sequenzen, die die von diesen Knoten repräsentierten Organismen
gehabt haben könnten. Diese Sequenzen werden so konstruiert,
daß die Sequenzen entlang des Baumes, während der vom Stammbaum
vorgegebenen evolutionären Entwicklung, möglichst wenigen
Mutationen unterworfen sind. Die Gesamtsumme aller im Baum nötigen
Mutationen ist dann das Maß für die Qualität des Baumes.
Von der Maximum-Parsimony-Methode wird versucht,
aus allen möglichen Stammbäumen denjenigen zu finden, für den
die geringste Anzahl an Mutationen nötig ist.
Diese Methode wurde ursprünglich für morphologische Daten entworfen
und hat sich bewährt, wenn sich die beobachteten Merkmale nur selten
ändern. Das gilt im allgemeinen für morphologische Daten.
Diese Methode scheitert jedoch, wenn die beobachteten Merkmale hochvariabel
sind oder sehr lange Kanten im gesuchten Baum vorkommen.
(Swofford and Olsen, 1990; Waterman, 1995)