Phylogenetische Stammbäume

 

Abbildung:   Gewurzelter phylogenetischer Baum

In Stammbaumanalysen konstruierte Stammbäume werden graphentheoretisch als binäre Bäume dargestellt (Abb. 1.4). Solche Bäume sind azyklisch verbundene, in diesem Fall ungerichtete Graphen aus einer Menge von Knoten, die mittels Kanten miteinander verbunden sind. In der Menge von Knoten hat jeder Knoten einen Grad $d \leq 3$, d.h. er ist nie mit mehr als drei weiteren Knoten verbunden. Ein Knoten repräsentiert die Wurzel (d=2) und jeder interne Knoten hat genau zwei Nachfolger und einen Vorgänger (d=3). Die internen Knoten repräsentieren gemeinsame Vorfahren an den Verzweigungspunkten der Artbildung. Bei den Blättern (d=1) handelt es sich um rezente Organismen. Die Kantenlängen geben eine Form von Zeit an, die zwischen den einzelnen Knoten liegt, wie z.B. in der Einheit Mutationen pro Generation. (Brandstädt, 1994; Waterman, 1995)

Es ist natürlich nicht klar, daß an einem Verzweigungspunkt immer genau zwei Arten entstanden sind. Diese Ungenauigkeit wird dadurch umgangen, daß man Kanten mit einer Länge null zuläßt. Dies bedeutet, daß die beiden adjazenten Knoten der ,,Nullkante`` denselben Vorfahren repräsentieren. Beide Knoten haben dann dieselben Merkmale, da die Evolution keine Zeit hatte, eines der Merkmale zu verändern. (Felsenstein, 1981)

   

Abbildung:   Zwei typische rekonstruierte phylogenetische Bäume. (a) ungewurzelt; (b) wurde mittels einer Außengruppe A gewurzelt

Ein zweites Problem ist, daß wir keine Möglichkeit haben, die Sequenzen des frühesten gemeinsamen Vorfahren, der Wurzel, zu bestimmen, um den Sitz des Ursprungs des Stammbaums zu bestimmen. Daher nimmt man einen Organismus oder eine Gruppe von Organismen, von denen bekannt ist, daß sie im Stammbaum einen gemeinsamen Vorfahren mit den anderen Organismen besitzen, der zeitlich vor dem Aufspalten der zu untersuchenden Gruppe existiert hat. Ein solcher Organismus bzw. eine solche Gruppe heißt Außengruppe, da sie außerhalb des eigentlich zu untersuchenden Bereichs liegt, und fungiert dann als Wurzel (Abb. 1.5b). Es handelt sich bei den gefundenen Bäumen eigentlich um sogenannte ungewurzelte Bäume (Abb. 1.5a). Auch die Sequenzen der anderen internen Knoten können heute im Normalfall nicht mehr bestimmt werden. Diese werden in Abhängigkeit von der benutzten Methode meist in irgendeiner Form für die Berechnung rekonstruiert. (Felsenstein, 1981; Swofford and Olsen, 1990)

Bei der Rekonstruktion phylogenetischer Stammbäume werden im Idealfall alle möglichen Bäume anhand eines vorgegebenen Kriteriums (z.B. Maximum Likelihood) untersucht, um sicher zu gehen, daß man auch den nach diesem Kriterium besten Baum findet. (Felsenstein, 1981, 1982; Swofford and Olsen, 1990)

Hierzu muß man allerdings wissen, daß für n Spezies

$$\prod^{n}_{k=3} (2k-5) = \frac{(2n-5)!}{2^{n-3}(n-3)!}$$

verschiedene ungewurzelte binäre Stammbäume existieren. Betrachtet man gewurzelte Stammbäume, so erhöht sich n um eins, da sich die Wurzel wie ein zusätzliches Blatt im Baum verhält. Dies bedeutet für die Analysen, daß für nur 10 Spezies schon über zwei Millionen ungewurzelter Stammbäume existieren. (Cavalli-Sforza and Edwards, 1967; Felsenstein, 1978)

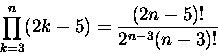
Aufgrund dieses immensen Wachstums der Anzahl der Bäume, ist es im allgemeinen nicht möglich, die Gesamtheit aller möglichen Bäume zu betrachten, um den optimalen Baum zu finden. Aus diesem Grund werden heuristische Verfahren verwendet, um die Anzahl der zu betrachtenden Bäume einzuschränken. Zwei häufig verwendete Verfahren sind das Clustering-Verfahren und das schrittweise Einfügen (Swofford and Olsen, 1990).

 Beim Clustering werden die Sequenzen oder Sequenzgruppen gesucht, die sich nach einem bestimmten Maß, meist der evolutionären Distanz zwischen den Sequenzen, am ähnlichsten sind. Diese bilden zusammen eine neue Gruppe und gehen als solche in das weitere Clustering ein. (Swofford and Olsen, 1990)

Beim schrittweisen Einfügen wird, angefangen mit einer kleinen Teilmenge der zu untersuchenden Taxa, der optimale Baum für diese Taxa bestimmt. Anschließend werden Schritt für Schritt weitere Taxa eingefügt und der, basierend auf dem vorher gefundenen Baum, nächste optimale Baum gesucht. (Felsenstein, 1981; Swofford and Olsen, 1990)

Bei beiden oben genannten Verfahren handelt es sich um Greedy-Verfahren, die sich Schritt für Schritt von einer lokal besten Entscheidung zur nächsten bewegen. Diese Verfahren sich vergleichbar mit den in der Informatik verwendeten Verfahren von Kruskal bzw. Prim zum Berechnen Minimaler Spannbäume (MSB) in Graphen (, )[persönliche Kommunikation]vingron-mitteilung.

Clustering entspricht hierbei der Methode von Kruskal, bei der die kürzeste verbindende Kante zwischen zwei Zusammenhangskomponenten im Graphen gesucht wird, die dann durch die gemeinsame Zusammenhangskomponente, hier Organismen-Gruppen, ersetzt werden. Dieses wird solange fortgeführt, bis alle Knoten des Graphen zu einer Zusammenhangskomponente verbunden sind (Cormen et al., 1990; Ottmann and Widmayer, 1993).

Prim's Algorithmus entspricht dem schrittweisen Einfügen. Hierbei wird die kürzeste Kante gesucht, die einen neuen Knoten mit einer bestehenden Zusammenhangskomponente verbindet. Dabei wird nur eine Zusammenhangskomponente, hier Bäume der bisher betrachteten Organismen, schrittweise vergrößert, bis alle Knoten enthalten sind (Cormen et al., 1990; Ottmann and Widmayer, 1993).