 |
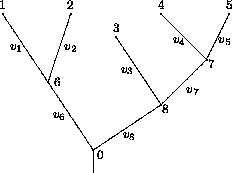
Für die Berechnung des Likelihood-Wertes benötigen wir ein Evolutionsmodell und eine hieraus resultierende Wahrscheinlichkeitsfunktion Pij(t). Hier wird das in Kap. 1.4.2 beschriebene generalisierte 2-Parameter-Modell von Kishino and Hasegawa (1989) verwendet. Als Stichprobe zur Berechnung dient ein vorgegebener Datensatz in Form eines Alignments der DNA-Sequenz. Die einzelnen Stichproben sind hier die Spalten des Alignments. Zusätzlich wird ein gegebener Stammbaum als Hypothese (Goldman, 1990) in der Analyse verwendet.
Wie schon oben erwähnt, gibt die Funktion Pij(t) die Wahrscheinlichkeit an, mit der eine Base aus dem Zustand i in einer Zeitspanne t in einen Zustand j übergeht. Die Zustände i und j entsprechen dabei einer der vier organischen Basen Adenin (A), Cytosin (C), Guanin (G) oder Thymin (T) bzw. Uracil (U) bei RNA-Sequenzen.
Zuerst wird der Likelihood-Wert eines Baumes für eine Spalte x im Sequenzalignment berechnet. Dieses geschieht rekursiv; daher definieren wir für die Berechnung des Likelihood-Wertes eines Teilbaumes, der mit dem Knoten k innerhalb der Phylogenie mit dem Sequenzstatus sk und den Nachfolgern i und j mit deren möglichen Sequenzstatus si und sj beginnt, wie folgt:
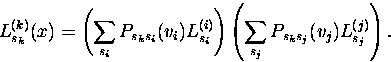 |
(4) |
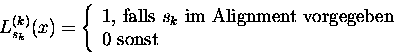 |
(5) |
Hieraus ergibt sich für die Berechnung des Likelihood-Wertes des gesamten Stammbaumes an dieser Sequenzposition:
| (6) |
Zur Berechnung des Likelihood-Wertes des Baumes über die gesamte
Stichprobe, bestehend aus den einzelnen Proben
![]() , werden die Likelihood-Werte für alle
n Spalten im Alignment miteinander multipliziert:
, werden die Likelihood-Werte für alle
n Spalten im Alignment miteinander multipliziert:
| |
(7) |
| |
(8) |
Durch die Gleichungen 4.9 bzw. 4.10 wird die Wahrscheinlichkeit berechnet, mit der die verwendeten Sequenzdaten den vorliegenden Baum mit seinen Kantenlängen unterstützen.
Die oben beschriebene Berechnung hängt von uns unbekannten Parametern, den Kantenlängen, ab. Sinn der Maximum-Likelihood-Methode ist, solche unbekannten Parameter anhand einer Stichprobe zu schätzen. Betrachten wir nun die Stichprobe als fest, dann hängt die Likelihood-Funktion nur noch von den Kantenlängen ab. Diese sollen so approximiert werden, daß der Likelihood-Wert des vorgegebenen Baumes sein Maximum erreicht. Wie diese Parameter geschätzt werden, wird nachfolgend beschrieben.