Analyse mit gewichtetem Datensatz

**Abbildung:** Verteilung der Basen des Plastidendatensatzes 2 auf 3 Gewichtsgruppen; Gewichtungsfunktion: 1/S; Anzahl Basen: 1429
$\begin{figure} ~\hfill \beginpicture \setcoordinatesystem units <1cm,0.4mm\gt ... ...188} [b] at 2.0 13.6 \put {193} [b] at 3.0 13.9 \endpicture \hfill~\end{figure}$

**Abbildung:** Verteilung der Basen des Plastidendatensatzes 1 auf 5 Gewichtsgruppen; Gewichtungsfunktion: 1/S; Anzahl Basen: 1429
$\begin{figure} ~\hfill \beginpicture \setcoordinatesystem units <1cm,0.4mm\gt ... ...{109} [b] at 3.0 8.0 \put {193} [b] at 5.0 13.9 \endpicture \hfill~\end{figure}$

**Abbildung:** Verteilung der Basen im Plastidendatensatz 1 auf die 10 Gewichtsgruppen; Gewichtungsfunktion: 1/S; Anzahl Basen: 1429
$\begin{figure} ~\hfill \beginpicture \setcoordinatesystem units <1cm,0.4mm\gt ... ...109} [b] at 5.0 8.0 \put {193} [b] at 10.0 13.9 \endpicture \hfill~\end{figure}$

Da die Sequenzstellen in rRNA sehr unterschiedliche Variabilität besitzen, wurde anhand des oben gefundenen Stammbaumes (Abb. 6.5) eine Gewichtung der Alignmentspalten mit 10 Gewichtsklassen vorgenommen (Abb. 6.8). Für den Datensatz mit 10 Gewichten ergab sich, nach zwei globalen Rearrangements und insgesamt 11536 untersuchten Bäumen, ein Baum mit einem Log-Likelihood-Wert von -19576,30 (Abb. 6.11). Jedes der bei den obigen Datensätzen durchgeführten Rearrangements umfaßte 4290 untersuchte Bäume.

Der so berechnete Baum in Abb. 6.11 zeigte eine interessante Veränderung zu dem ungewichteten Baum (Abb. 6.5). Die Gruppe der Cyanellen divergierte nun im Stammbaum nicht mehr vor, sondern nach den Chloroplasten.

Um die Auswirkungen von solchen Gewichtsveränderungen weiter zu untersuchen, wurde der Datensatz anhand des oben gefundenen Stammbaumes mit weiteren unterschiedlichen Gewichten (mit 3 und 5 Gewichten) belegt. Die Verteilung der Basenanzahl auf die einzelnen Gewichte sind in den Abbildungen 6.6 und 6.7 dargestellt. Zu allen gewichteten Datensätzen wurden Stammbäume berechnet.

Alle nicht explizit noch einmal aufgeführten Daten und Parameter sind identisch zu den schon oben gefundenen. Für den Datensatz mit drei Gewichten ergab sich nach zwei globalen Rearrangements und insgesamt 11484 untersuchten Bäumen ein Baum mit dem Log-Likelihood-Wert von -18980,62 (Abb. 6.9).

**Abbildung:** Phylogenetischer Stammbaum der Plastidenentwicklung; berechnet aus 16S rRNA-Sequenzen (Datensatz *plast1* ) mit 3 Gewichtsgruppen mittels `pfastDNAml`
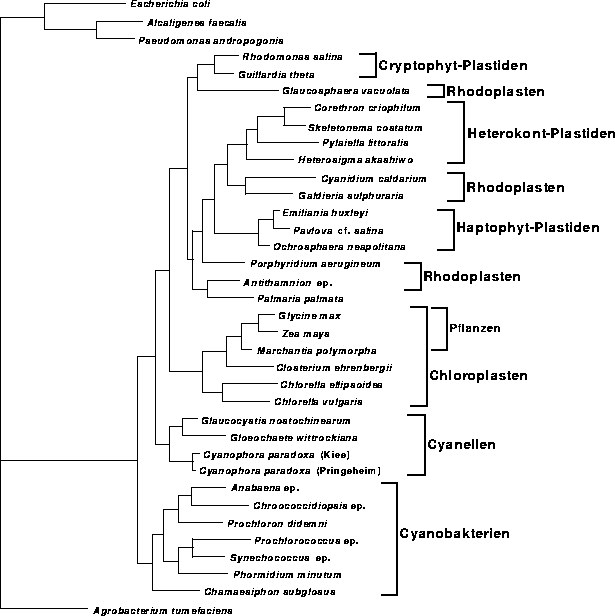$\begin{figure} \centering \epsfig {file=images/figpl1wei3.eps,width=13.7cm} \end{figure}$

Für den Datensatz mit 5 Gewichten ergab sich nach sechs globalen Rearrangements und insgesamt 28668 untersuchten Bäumen ein Baum mit dem Log-Likelihood-Wert von -19276,75 (Abb. 6.10).

**Abbildung:** Phylogenetischer Stammbaum der Plastidenentwicklung; berechnet aus 16S rRNA-Sequenzen (Datensatz *plast1* ) mit 5 Gewichtsgruppen mittels `pfastDNAml`
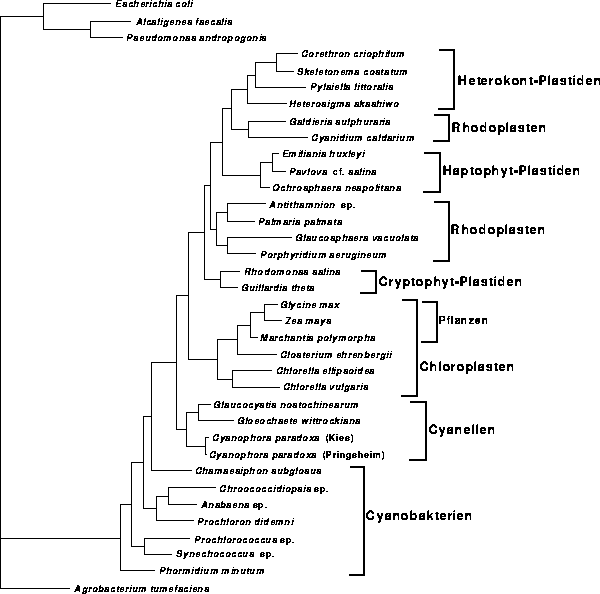$\begin{figure} \centering \epsfig {file=images/figpl1wei5.eps,width=13.7cm} \end{figure}$

Anhand des letzten mit 10 Gewichten gewichteten Datensatzes wurde außerdem eine Bootstrap-Analyse mit 100 Pseudostichproben durchgeführt, ein Konsensusbaum erstellt und die Bootstrap-Werte $\gt 60\%$ in den Baum in Abb. 6.11 eingefügt.

**Abbildung:** Phylogenetischer Stammbaum der Plastidenentwicklung; berechnet aus 16S rRNA-Sequenzen (Datensatz *plast1* ) mit 10 Gewichtsgruppen mittels `pfastDNAml`; nur Bootstrap-Werte über $60\%$ wurden an den entsprechenden Kanten eingefügt
$\begin{figure} \centering \epsfig {file=images/figpl1wei10.eps,width=13.7cm} \end{figure}$