


Next: Die Maximum-Likelihood-Methode zur Rekonstruktion
Up: Modellierung evolutionärer Prozesse
Previous: Markov-Prozesse
Es gibt unterschiedliche Modelle,
mit denen der evolutionäre Prozeß beschrieben wird.
Das hier verwendete Modell ist das generalisierte 2-Parameter-Modell
von Kishino and Hasegawa (1989). Es wird im Programmpaket PHYLIP seit Version 2.6
verwendet und wurde mit in das Programm fastDNAml, basierend auf
PHYLIP Version 3.3, übernommen.
Dieses Modell findet auch unverändert in pfastDNAml Anwendung.
Das generalisierte 2-Parameter-Modell modelliert
den Evolutionsprozeß als reversiblen Markov-Prozeß
(s. Kap. 4.1.1).
Das Modell liefert uns eine Wahrscheinlichkeitsmatrix
| 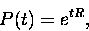 |
(1) |
aus der die Wahrscheinlichkeit eines Basenaustausches in einem Zeitraum
t entnommen werden kann. Bei R handelt es sich um die Ratenmatrix
bzw., um den wahrscheinlichkeitstheoretischen Terminus zu gebrauchen,
Generatormatrix,
in der die einzelnen Substitutionsraten rij von einer Base
i in eine Base j enthalten sind. Dieses rij errechnet sich wie
folgt:
| 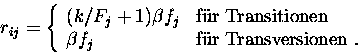 |
(2) |
Dabei gibt fj die Basenfrequenz der Base j, Fj die Frequenz des Basentyps
(Purin oder Pyrimidin) an. 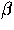 entspricht der Transversionsrate pro
Base, während k die Rate
entspricht der Transversionsrate pro
Base, während k die Rate 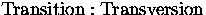 angibt.
angibt.
Die Ratenmatrix lautet also wie folgt:
| ![\begin{displaymath}
\scriptstyle\left[ \begin{array}
{cccc}
\scriptstyle -\left...
...f_A + Y_C \cdot f_C + f_G\right)\beta \ \end{array} \right]
\end{displaymath}](img33.gif) |
(3) |
Hierbei entsprechen
Die Matrizen sind so angelegt, daß sich die Inhalte
einer Zeile der Generatormatrix R zu und die Inhalte der
Wahrscheinlichkeitsmatrix P zu 1 (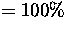 ) aufaddieren.
) aufaddieren.
Die Wahrscheinlichkeitsmatrix P(t) wird in der nachfolgend
beschriebenen Maximum-Likelihood-Methode verwendet, um die
Wahrscheinlichkeit Pij(t) für einen Basenaustausch von
i nach j in einem Zeitraum t zu berechnen.
Vorteil der Modellierung des Evolutionsprozesses mit Matrizen
ist es, daß bei der Berechnung der Wahrscheinlichkeit einer
Basensubstitution alle möglichen Übergangszustände
automatisch mit berücksichtigt werden.
D.h. es werden auch die Wahrscheinlichkeiten der verschiedenen
Zwischenzustände mit berücksichtigt.



Next: Die Maximum-Likelihood-Methode zur Rekonstruktion
Up: Modellierung evolutionärer Prozesse
Previous: Markov-Prozesse
Heiko Schmidt
7/17/1997
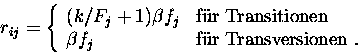
![\begin{displaymath}
\scriptstyle\left[ \begin{array}
{cccc}
\scriptstyle -\left...
...f_A + Y_C \cdot f_C + f_G\right)\beta \ \end{array} \right]
\end{displaymath}](img33.gif)
![]() ) aufaddieren.
) aufaddieren.