


Next: Generalisiertes 2-Parameter-Modell
Up: Modellierung evolutionärer Prozesse
Previous: Modellierung evolutionärer Prozesse
Um den Prozeß von Basensubstitutionen in der DNA im Laufe der Evolution
beschreiben zu können, werden im allgemeinen reversible
Markov-Prozesse herangezogen.
Bei Markov-Prozessen handelt es sich um stochastische Prozesse,
für deren Verhalten in der Zukunft lediglich die Werte in der
Gegenwart, nicht aber die in der Vergangenheit eine Rolle spielen.
Die Wahrscheinlichkeit, daß ein bestimmter Zustand zu einem Zeitpunkt
t > tm eintritt, wenn die Zustände zu den Zeitpunkten
 bekannt sind, ist bei einem Markov-Prozeß
gleich groß wie die Wahrscheinlichkeit des Eintretens des
Zustands zum Zeitpunkt
t > tm, wenn nur der Zustand zum Zeitpunkt tm bekannt ist.
bekannt sind, ist bei einem Markov-Prozeß
gleich groß wie die Wahrscheinlichkeit des Eintretens des
Zustands zum Zeitpunkt
t > tm, wenn nur der Zustand zum Zeitpunkt tm bekannt ist.
Dieses bedeutet für den Evolutionsprozeß, daß Basensubstitutionen
zufällig passieren, unabhängig davon welche Mutation zuletzt
aufgetreten ist.
Bei einem reversiblen Markov-Prozeß gilt noch zusätzlich, daß
die Wahrscheinlichkeit 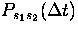 , mit der ein Zustand s1
nach einer Zeitspanne
, mit der ein Zustand s1
nach einer Zeitspanne 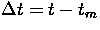 mit t > tm in einen
Zustand s2 übergegangen ist, gleich groß ist wie die Wahrscheinlichkeit
mit t > tm in einen
Zustand s2 übergegangen ist, gleich groß ist wie die Wahrscheinlichkeit
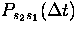 , mit der der Zustand s2 nach derselben Zeitspanne
, mit der der Zustand s2 nach derselben Zeitspanne
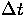 in einen Zustand s1 übergegangen ist.
in einen Zustand s1 übergegangen ist.
Die Annahme eines reversiblen Markov-Prozesses ist notwendig, um mit
ungewurzelten Bäumen rechnen zu können.
Außerdem konstruieren wir die Stammbäume von bekannten, rezenten
Sequenzen in die Vergangenheit, was beim
herkömmlichen Markov-Prozeß nicht unterstützt wird.
(Felsenstein, 1981; Schneider, 1991)



Next: Generalisiertes 2-Parameter-Modell
Up: Modellierung evolutionärer Prozesse
Previous: Modellierung evolutionärer Prozesse
Heiko Schmidt
7/17/1997
![]() , mit der ein Zustand s1
nach einer Zeitspanne
, mit der ein Zustand s1
nach einer Zeitspanne ![]() mit t > tm in einen
Zustand s2 übergegangen ist, gleich groß ist wie die Wahrscheinlichkeit
mit t > tm in einen
Zustand s2 übergegangen ist, gleich groß ist wie die Wahrscheinlichkeit
![]() , mit der der Zustand s2 nach derselben Zeitspanne
, mit der der Zustand s2 nach derselben Zeitspanne
![]() in einen Zustand s1 übergegangen ist.
in einen Zustand s1 übergegangen ist.